Patrolling is the task of continuously monitoring an environment over a long period of time. Many multi-robot applications, including disaster response, security tasks as well as exploration and mapping, can be represented as a patrolling problem. In our recent paper, we investigated multi-robot patrolling with limited connectivity among robots and developed approximate algorithms for efficiently solving this complex problem.
We consider a multi-robot patrolling scenario with intermittent connectivity constraints, ensuring that robots’ data finally arrive at a base station. In particular, each robot traverses a closed tour periodically and meets with the robots on neighboring tours to exchange data. We model the problem as a variant of the min-max vertex cycle cover problem (MMCCP), which is the problem of covering all vertices with a given number of disjoint tours such that the longest tour length is minimal. Many multi-robot patrolling applications require a set of robots to travel around in the environment and visit points of interest (sensing locations [SL]) periodically. The idleness of an SL at a certain time instant is defined as the time that passed since the last visit of the SL by a robot.
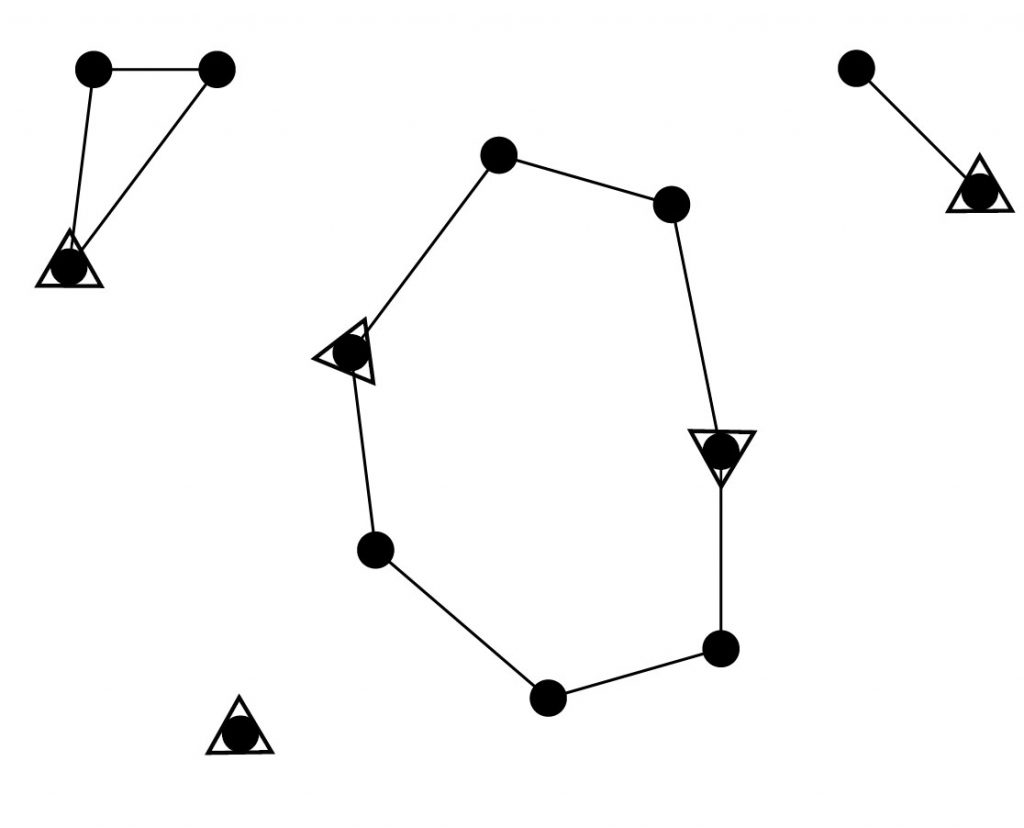
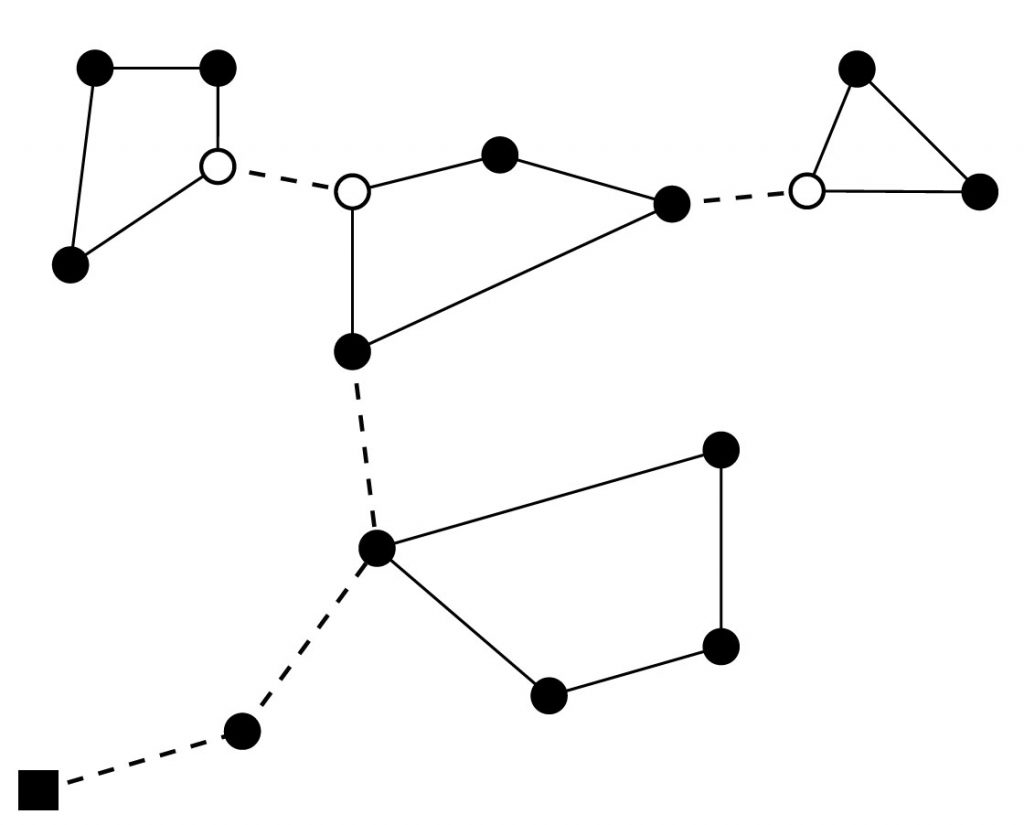
We consider two problems: minimum idleness mixed strategy multi-robot patrolling (MIMP) and minimum idleness connectivity-constrained multi-robot patrolling (MICP). MIMP describes the problem of partitioning a graph and finding tours on the partitions such that the worst idleness is minimized. MICP describes the problem of partitioning a graph and finding tours on partitions such that robots can also communicate and the data arrives at a base station. This might require introducing vertices, which are not SLs, to tours such that robots are within communication range.
The computational complexity of exactly solving these problems restrains practical applications, and therefore we develop approximate algorithms. Our simulation experiments on 10 vertices and up to
3 robots compare the results of different solution approaches (including solving the MILP formulation) and show that our greedy algorithm can obtain an objective value close to the one of the MILP formulations but requires much less computation time. Experiments on instances with up to 100 vertices and 10 robots indicate that the greedy approximation algorithm tries to keep the length of the longest tour small by extending smaller tours for data exchange.
Jürgen Scherer, Angela P. Schoellig, Bernhard Rinner. Min-max vertex cycle covers with connectivity constraints for multi-robot patrolling. Robotics and Automation Letters. 2022 (early access).